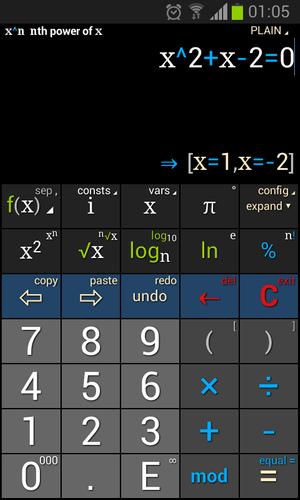
強力な科学的計算機、ファクト、マトリックス、積分、導関数
Primecalc -Free Scientific Symbolic Calculator
-70関数、20の数学定数、最大6つの変数
- 新しい機能と定数はユーザーが定義できます
- 複雑な数値をサポートします
- マトリックス、ベクトル、セット、および計算
- 数学的方程式を解決します
- 積分と導関数を計算します
- ステップバイステップの計算
- そしてもっと
サポートされている機能、演算子、および数学定数:
算術:
演算子 +、 - 、×、÷、%
x^n -n xのn
√(x) - xの平方根
√(n、x) - xのn番目のルート
ln(x) - xの自然対数
log(x) - xの対数ベース10
log(n、x) - ベースnへのxの対数
∑(f(x)、imin、imax) - イミンからimaxへのf(x)の合計
∏(f(x)、imin、imax) - イミンからimaxへのf(x)の積
数学的分析:
∫(f(x)) - f(x)の不定積分
∫(f(x)、xmin、xmax) - xminからxmaxへのf(x)の明確な積分
∂(f(x)) - f(x)の誘導体
lim(f(x)、c) - xがcに近づくときのf(x)の制限
方程式解決:
多項式の表現-X^2+3x -2 = 0
= - 多項式方程式演算子
数値関数:
m mod n -m÷nの残り
gcd(m、n) - mとnの最大の共通除数
LCM(M、N) - MおよびNの最小一般的な倍数
ABS(n) - nの絶対値
round(n) - nに最も近い整数
frac(n) - nの分数部分
床(n) - nの床値
天井(n) - nの天井値
複雑な数:
表現-5+2i
Re(c) - 複雑な数の実際の部分c
IM(c) - 複雑な数の想像上の部分c
統計:
中央値([a]) - [a]の中央値
gmean([a]) - [a]の幾何平均
Amean([a]) - [a]の算術平均
Randi(n) - 0からnのランダム整数
RANDR -0から1のランダムリアル
番号理論:
Harmonicn(n) - n番目の高調波番号
組み合わせ:
n! - nの要因
二項(n、k) - 二項係数
多項(N1、N2、...) - 多項係数
Catalann(n)-Nthカタロニア番号
フィボナッチ(n)-Nthフィボナッチ数
三角関数:
sin(x)、cos(x)、tan(x)
sec(x)、csc(x)、cot(x)
asin(x)、acos(x)、atan(x)、acot(x)
双曲線機能:
sinh(x)、cosh(x)、tanh(x)
Arsinh(x)、Arcosh(x)、Artanh(x)
マトリックス:
表現 - [[1,2]、[3,4]]
[M1]⋅[M2] - [M1]と[M2]の産物
Tran([M]) - 転置[M]
ctran([m]) - 共役と転置[m]
逆([m]) - 反転[m]
det([m]) - [m]の決定要因
TR([M]) - [M]のトレース
mpow([m]、n) - n番目のマトリックス電力[m]
番号セット:
表現 - [1,2]
Union([a1]、[a2]) - 2セットの組合
intersec([a1]、[a2]) - 2セットの交差
max([a]) - [a]の最大の要素
min([a]) - [a]の最小要素
定数:
π-数字pi
E-オイラーの番号
I-想像上のユニット
∞-無限
γ-オイラー - マシェロニ定数
G-カタロニアの定数
A-グレイッシャー - キンケリン定数
φ-ゴールデン比
κ-キンキンの定数
C₂ -Twin Prime Constant
ζ₃-アペリの定数
B₄-プライムクアッドレットのブルン定数
B₂ -Twin PrimesのBrunの定数
eb -erdős– borwein constant
Δ-フェイゲンバウム最初の定数
α-フェイゲンバウム2番目の定数
bl- legendreの定数
M₁ -Meissel -Mertens Constant



February 17, 2026
February 17, 2026

February 17, 2026
February 16, 2026
February 16, 2026
February 16, 2026

February 16, 2026
February 16, 2026
February 16, 2026
February 16, 2026