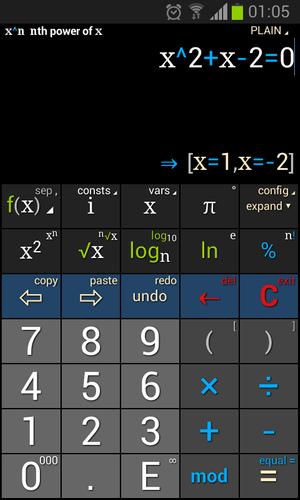
강력한 과학 계산기, 연기, 매트릭스, 적분 및 파생 상품
PRIMECALC- 자유 과학적 상징적 계산기
-70 개의 기능, 20 개의 수학 상수 및 최대 6 개의 변수
- 새로운 기능과 상수는 사용자가 정의 할 수 있습니다.
- 복소수를 지원합니다
- 매트릭스, 벡터, 세트 및 계산
- 수학적 방정식을 해결합니다
- 적분 및 파생 상품을 계산합니다
-단계별 계산
- 그리고 더 많은
지원되는 기능, 연산자 및 수학 상수 :
산수:
연산자 +, -, ×, ÷, %
x^n- x의 전력
√ (x) - x의 제곱근
√ (n, x) - x의 n 번째 루트
ln (x) - x의 자연 로그
log (x) - x의 로그에서베이스 10
log (n, x) - x에서 base n의 로그
장
짐
수학적 분석 :
∫ (f (x)) - f (x)의 무기한 적분
짐
∂ (f (x)) - f (x)의 미분
lim (f (x), c) - x에 접근 할 때 f (x)의 한계 c
방정식 해결 :
다항식의 표현 -x^2+3x -2 = 0
= - 다항식 방정식 연산자
수치 기능 :
m 모드 n- 나머지 m ÷ n
GCD (M, N) - M 및 N의 가장 큰 일반적인 제수
LCM (M, N) - 최소한의 M 및 N
ABS (N) - N의 절대 값
라운드 (n) - n에 가장 가까운 정수
frac (n) - n의 분수 부분
바닥 (n) - n의 바닥 값
CEIL (N) - N의 천장 값
복소수 :
표현 -5+2I
Re (c) - 복소수의 실제 부분 c
IM (C) - 복소수의 가상 부분 c
통계:
중앙값 ([a]) - [a]의 중앙값
gmean ([a]) - [a]의 기하학적 평균
Amean ([a]) - [a]의 산술 평균
randi (n) - 0에서 n까지의 랜덤 정수
randr- 랜덤 레알 0에서 1까지
숫자 이론 :
고조파 (N) - Nth 고조파 번호
조합 :
N! - n의 factorial
이항 (n, k) - 이항 계수
다국적 (N1, N2, ...) - 다중 생물 계수
Catalann (N) - Nth 카탈로니아어 번호
fibonacci (n) - nth fibonacci 번호
삼각법 :
sin (x), cos (x), tan (x)
SEC (X), CSC (X), COT (X)
asin (x), acos (x), atan (x), acot (x)
쌍곡선 기능 :
sinh (x), cosh (x), tanh (x)
arsinh (x), Arcosh (x), artanh (x)
매트릭스 :
표현 - [[1,2], [3,4]]
[M1] ⋅ [M2] - [M1] 및 [M2]의 제품
tran ([m]) - 전환 [m]
ctran ([m]) - 컨쥬 게이트 및 전환 [M]
역 ([m]) - 반전 [m]
det ([m]) - [m]의 결정 요인
tr ([m]) - [m]의 흔적
mpow ([m], n) - [m]의 nth 행렬 전력
번호 세트 :
표현 - [1,2]
Union ([A1], [A2]) - 두 세트의 연합
Intersec ([a1], [a2]) - 두 세트의 교차점
max ([a]) - [a]의 가장 큰 요소
최소 ([A]) - [A]의 가장 작은 요소
상수 :
π- 숫자 pi
E -Euler의 번호
I- 상상의 단위
∞ - 무한대
γ -Euler – Mascheroni 상수
G- 카탈로니아의 상수
A- 글레이 쉬 - 킨 켈린 상수
φ- 황금 비율
κ- 킨친의 상수
C₂- 트윈 프라임 상수
하거나 Apéry의 상수
B₄- Brun 's Constant for Prime Ququplets
B₂- Brun 's Constant for Twin Primes
eb -erd–s – orborwein constant
δ- Feigenbaum 첫 번째 상수
α- Feigenbaum 두 번째 상수
BL- Legendre 's Constant
m ₁ - Meissel – Mertens가 일정합니다



February 17, 2026
February 17, 2026

February 17, 2026
February 16, 2026
February 16, 2026
February 16, 2026

February 16, 2026
February 16, 2026
February 16, 2026
February 16, 2026