How Long Wait? Little's Law

アプリは、キューイング理論におけるリトルの法則を使用して、推定待ち時間を計算します。

このアプリを選択していただきありがとうございます！

[アプリ]

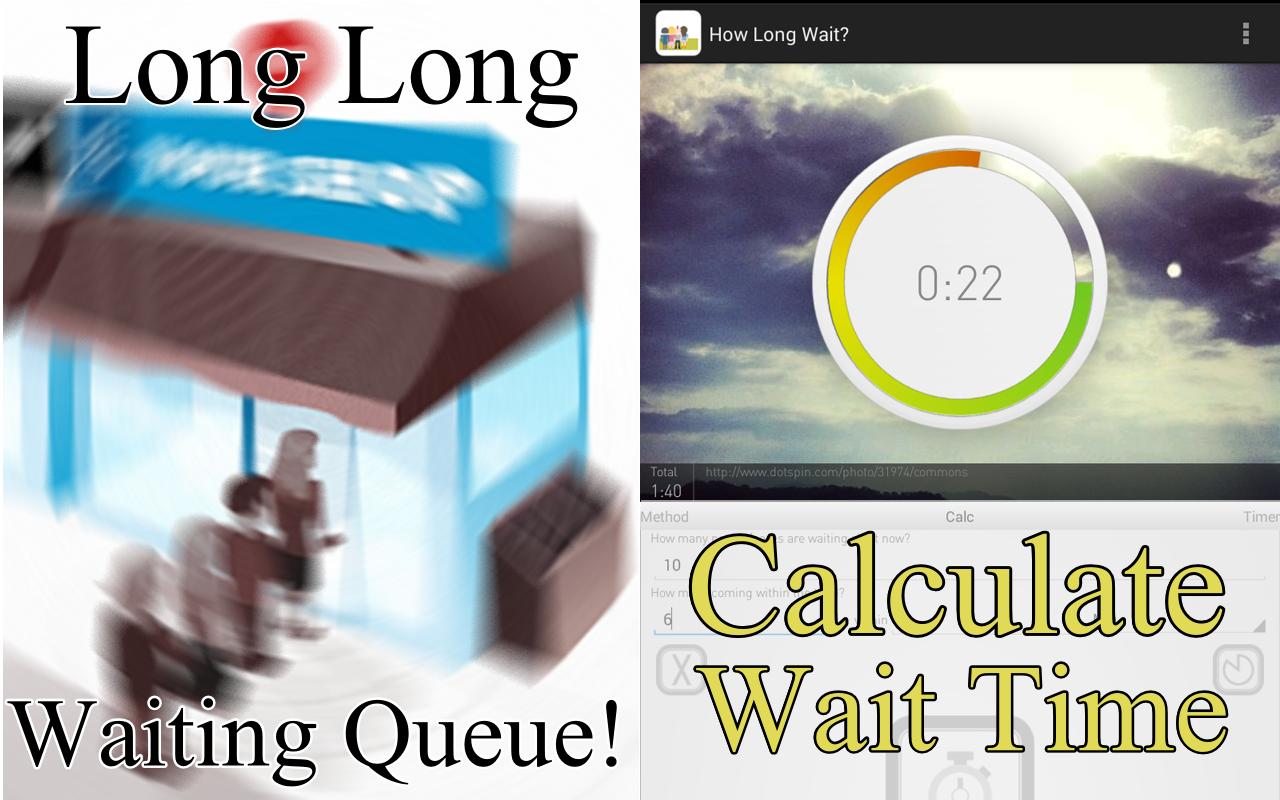
時々、私たちはキューで待たなければなりません…

どれくらい待たなければならないかを見積もることができたらいいと思ったことはありますか？

アプリは、キューイング理論におけるリトルの法則を使用して、推定待ち時間を計算します。

要件は、キューの長さが時間と非領土では変わらないということです。

このアプリがあなたの不満を少し癒すことを願っています:-)

[特徴]

使用が簡単で直感的な、大きなボタンとスワイプ

段階的な時期の理解可能な進行状況表示

時間内の人/ペアの数を数えるためのタイマー関数

進行時間形式の複数の選択肢

アニメーションの待機時間中に壁紙を更新します

待機時間が完了したときの通知。

お友達と見積もる待ち時間を共有してください！

タブレットのサポート、ポートレート、風景

広告なし（有料版用）

オフライン利用可能（有料版用）

[リトルの法則]

l =人/ペアの数

λ=人/ペアの到着率

w =待機時間を推定します

リトルの法則の公式はそうです

l =λxw

λは、有効到着率とも呼ばれます。

ユニット時間ごとに何人/ペアが来るかを示しています

そして、値が高いほど、より多くの人/ペアが来るでしょう。

ポアソン分布では、平均レートに相当します。

法律または公式は、1961年のジョン・リトル教授（MIT）による定理です。

法律は、到着プロセスの分布に影響されないため、かなり普遍的です。

サービスの配布、サービス注文。

[リトルの法律例1]

-10人が店で待っています

-4人が1分で到着しました

リトルの法則

L = 10

λ= 4

w = l /λ= 10/4 = 2.5

回答：待機する2分30秒

[リトルの法律例2]

- キャッシュデスクで8人が待っています

- 2人が10秒で到着しました

リトルの法則

L = 8

λ= 2

w = l /λ= 8/2（10秒単位時間）

回答：待機する40秒

最新バージョン0.2.0.0の新しいもの