该应用程序在排队理论中使用Little's Wraw计算估计等待时间。
感谢您选择此应用！
[应用程序]
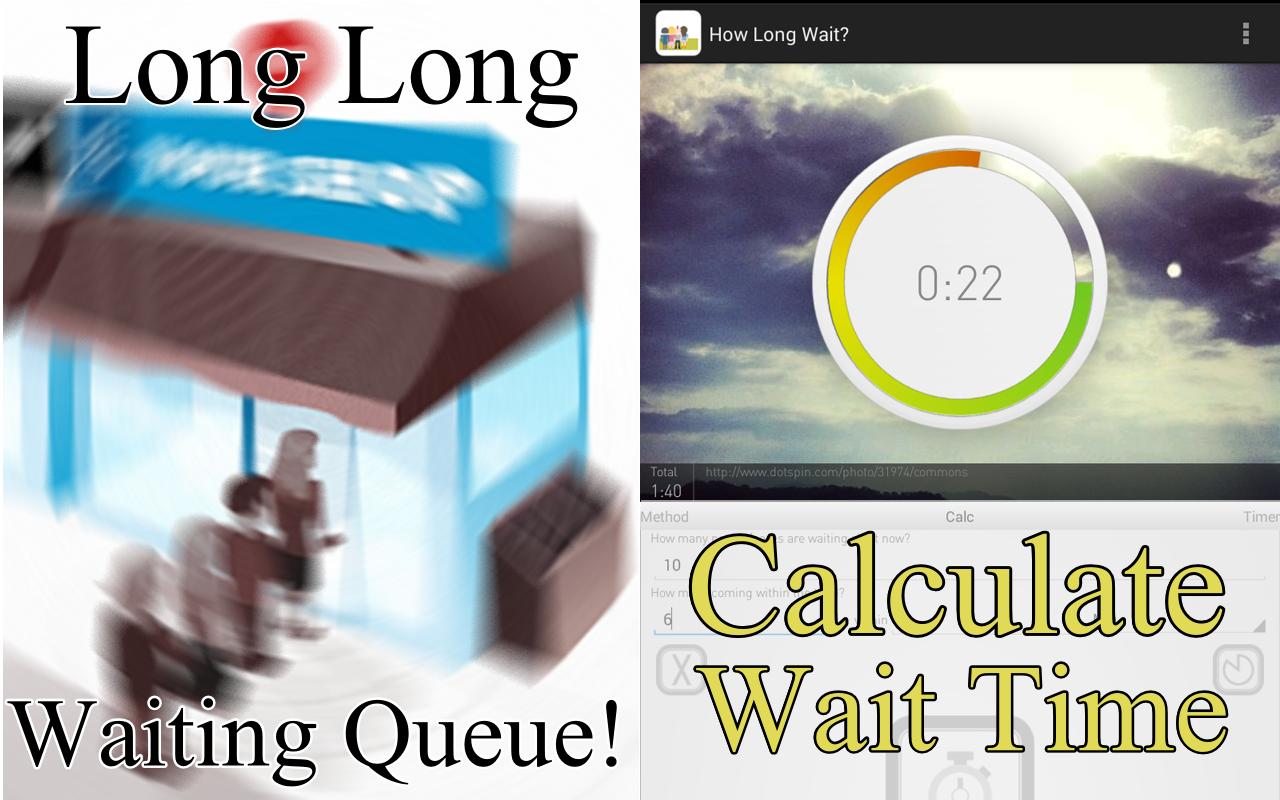
有时我们必须在队列中等待…
您是否曾经认为如果我能估计我必须等待多长时间，那会很好？
该应用程序在排队理论中使用Little's Wraw计算估计等待时间。
要求是队列的长度不会随着时间而变化，也不会变化。
希望此应用程序能够治愈您的不满:-)
[特征]
易用且直观的使用，大按钮和滑动
等待时间的可理解进度显示以供等待时间
计时器功能，用于计算及时的人/对数量
进度时间格式多种选择
在等待动画的等待时间更新壁纸
等待时间完成时通知。
与您的朋友分享估计等待时间！
平板电脑的支撑，肖像和景观
没有广告（用于付费版本）
离线可用（用于付费版本）
[小定律]
l =人的数量
λ=人/对的到达率
W =估计等待时间
小法则的公式是
l =λx w
λ也称为有效到达率。
它显示了单位时间会有多少人/对
价值越高，人/对就会越多。
在泊松分布中，它等效于平均速率。
法律或公式是1961年约翰·利特尔（MIT）教授的定理。
法律是相当普遍的，因为它不受到达过程分布的影响，
服务分配，服务订单。
[小法则示例1]
- 有10个人在商店里等待
- 有4人在1分钟内到达
根据小法则，
L = 10
λ= 4
w = l /λ= 10/4 = 2.5
答：2分钟30秒等待
[小法则示例2]
- 8个人在收银台等着
-2人在10秒内到达
根据小法则，
L = 8
λ= 2
w = l /λ= 8/2（10秒单位时间）
答：40秒等待
July 27, 2025
July 27, 2025
July 27, 2025
July 27, 2025
July 27, 2025
July 27, 2025
July 26, 2025
July 26, 2025
July 26, 2025
July 26, 2025
下载 APK(3.89MB)