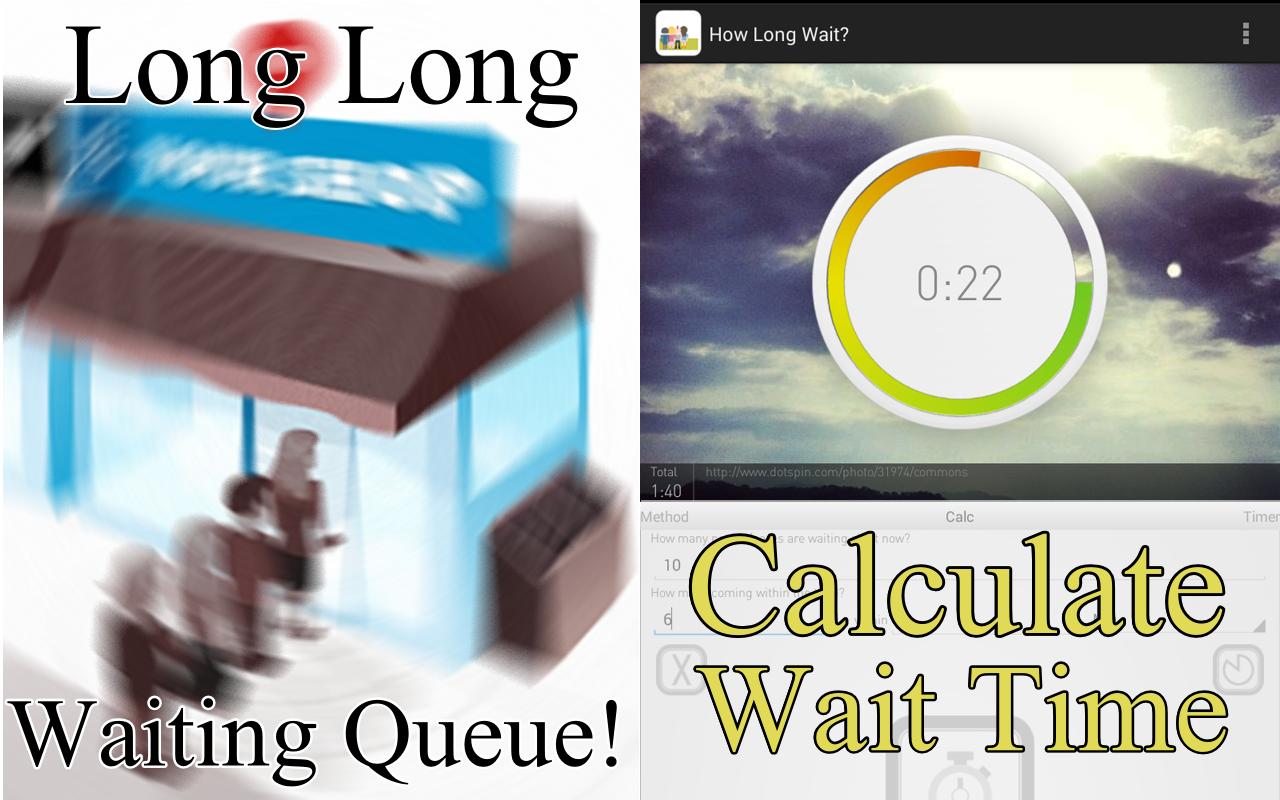
該應用程序在排隊理論中使用Little's Wraw計算估計等待時間。
感謝您選擇此應用！
[應用程式]
有時我們必須在隊列中等待…
您是否曾經認為如果我能估計我必須等待多長時間，那會很好？
該應用程序在排隊理論中使用Little's Wraw計算估計等待時間。
要求是隊列的長度不會隨著時間而變化，也不會變化。
希望此應用程序能夠治愈您的不滿:-)
[特徵]
易用且直觀的使用，大按鈕和滑動
等待時間的可理解進度顯示以供等待時間
計時器功能，用於計算及時的人/對數量
進度時間格式多種選擇
在等待動畫的等待時間更新壁紙
等待時間完成時通知。
與您的朋友分享估計等待時間！
平板電腦的支撐，肖像和景觀
沒有廣告（用於付費版本）
離線可用（用於付費版本）
[小定律]
l =人的數量
λ=人/對的到達率
W =估計等待時間
小法則的公式是
l =λx w
λ也稱為有效到達率。
它顯示了單位時間會有多少人/對
價值越高，人/對就會越多。
在泊松分佈中，它等效於平均速率。
法律或公式是1961年約翰·利特爾（MIT）教授的定理。
法律是相當普遍的，因為它不受到達過程分佈的影響，
服務分配，服務訂單。
[小法則示例1]
- 有10個人在商店裡等待
- 有4人在1分鐘內到達
根據小法則，
L = 10
λ= 4
w = l /λ= 10/4 = 2.5
答：2分鐘30秒等待
[小法則示例2]
- 8個人在收銀台等著
-2人在10秒內到達
根據小法則，
L = 8
λ= 2
w = l /λ= 8/2（10秒單位時間）
答：40秒等待
June 5, 2025
June 5, 2025
June 5, 2025
June 5, 2025
June 5, 2025
June 5, 2025
June 4, 2025
June 4, 2025
June 4, 2025
June 4, 2025
下載 APK(3.89MB)